導讀：

以后如果你看到量子計算機的新聞，千萬不要問“計算能力跟我的電腦比起來怎么樣”或者“打游戲會卡嗎”，人家一聽就知道你很外行。如果你問“它針對的是哪個數學問題，把計算量從什么改進到了什么”，人家就知道你是懂行的了。——一般人我不告訴他！

前文參見： 

你完全可以理解量子信息（1） | 袁嵐峰

你完全可以理解量子信息（2-3） | 袁嵐峰

你完全可以理解量子信息（4-5） | 袁嵐峰）

你完全可以理解量子信息（6） | 袁嵐峰）

你完全可以理解量子信息（7） | 袁嵐峰

八、量子信息的優勢

從以上內容可以看出，量子信息跟經典信息相比有很大的優勢。

首先是一個顯而易見的優勢。前面比喻過：經典比特是“開關”，只有開和關兩個狀態，而量子比特是“旋鈕”，有無窮多個狀態。旋鈕的信息量顯然比開關大得多。

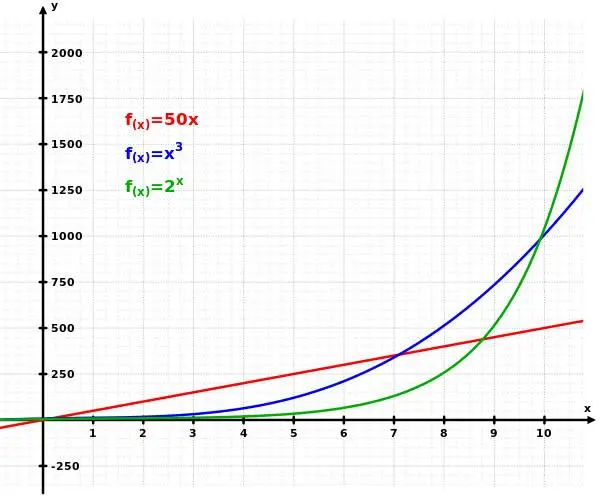
還有一個稍微復雜一點的優勢。一個包含n個經典比特的體系，總共有2^n個狀態。想知道一個函數在這個n比特體系上的效果，需要對這2^n個狀態都計算一遍，總共要2^n次操作。當n很大的時候，2^n是一個巨大的數字。指數增長是一種極快的增長，比n的任何多項式都快。比如說，2^n比n的10000次方增長得還要快。

對n個量子比特的體系，卻有一個巧妙的辦法。使每個量子比特都處于自己的|+> =(|0> + |1>)/√2態，那么整個體系的狀態就是|++…+> = (|00…0>+ |00…1> + … + |11…1>) /2^(n/2)。（根據定義就可以知道，這是個直積態，不是糾纏態，雖然它確實是一個疊加態。糾纏態和疊加態是兩個概念。）仔細看看你會發現，0和1的所有長度為n的組合都出現在其中，總共有2^n項，剛好對應n個經典比特的2^n個狀態。對這個疊加態做一次操作，得到的就是所有2^n個結果的疊加態。量子比特的一次操作，就達到了經典比特2n次操作的效果！

但在歡呼之前，我們需要認清，這個巨大的優勢并不容易利用。因為所有2n個結果是疊加在一起的，讀取出來需要做測量，而一做測量就只剩下一個結果，其余的結果都被破壞了。所以我們只能把這個優勢稱為潛在的巨大優勢，真要利用它，需要非常巧妙的算法。

這樣的算法只對少數的問題能夠設計出來，后面會舉一些例子，如“因數分解”。有些科普文章把量子計算機描寫成無所不能，快成神了，這是重大的誤解。量子計算機的強大，是與問題相關的，只針對特定的問題。

九、量子信息的應用

前面說過，量子信息的研究內容包括量子通信和量子計算。從這兩個名字我們立刻就可以發現，量子信息還沒有進入生活，因為大家都還在用經典的電腦和手機呢。具體地說，量子通信已經有了一些實際應用，量子衛星就是做相關實驗的。而量子計算的發展程度要低得多，還處于演示階段，尚未造出有實用價值的量子計算機。

量子信息究竟能用來干什么呢？下面我們來介紹量子信息的四項應用。在量子計算方面，有量子因數分解（破解最常用的密碼體系）和量子搜索（用途最廣泛的量子算法）。在量子通信方面，有量子隱形傳態（“傳送術”，最富有科幻色彩的應用）和量子密碼術。在所有這些應用中，量子密碼術是目前唯一接近實用的，但這一個就非常重要，足以表現量子信息的價值了。

十、量子因數分解和密碼破解

所謂因數分解，就是把一個合數分解成質因數的乘積，例如21 = 3 × 7。因數分解是數學中的經典難題。

你也許會問，這有什么難的？你當然不管三七二十一就能分解21，但請試試看分解2^67 - 1 =147,573,952,589,676,412,927。這是個18位數。1644年（明朝滅亡的那一年），法國數學家梅森（Marin Mersenne）提出它是一個質數。在那之后的很長時間里，人們都這么認為。直到1903年（清朝都快亡了），人們才發現它是一個合數，等于193,707,721 ×761,838,257,287。耗了一個朝代！

讓我們想想，如何分解一個數字N。最容易想到的算法，是從2開始往上，一個一個地試驗能否整除N，一直到N的平方根為止。如果N用二進制表示是個n位數，即N約等于2n，那么嘗試的次數大致就是2n/2。這是指數增長的計算量，前面說過，指數增長是一個災難。

在計算機科學中，把計算量指數增長的問題稱為“不可計算的”，把計算量多項式增長的問題稱為“可計算的”。不可計算的意思并不是計算機不能算，而是計算量增長得太快，很容易就達到“把全世界的計算機集中起來算幾十億年都無法得出結果”的程度。

當然，計算量是跟算法有關的，你可以尋找效率更高的算法，也應該這么做。對于因數分解，“從2開始一個一個試”并不是最聰明的算法。在經典計算機的框架中，目前最好的算法叫做“數域篩”，計算量有所減少，但仍然是指數增長。

“艾數學”同學，你想問數域篩的計算量具體是多少？一般人我不告訴他，答案是exp[O(n^(1/3) log^(2/3)n)]（在數學中，大寫字母O后面跟一個式子，表示結果跟這個式子具有同樣的數量級）。

這樣的計算量是什么概念？如果計算機一秒做1012次運算，那么分解一個300位的數字需要15萬年，分解一個5000位的數字需要……50億年！地球的年齡也不過是46億年而已！

由此可以看出因數分解的一個特點：它的逆操作，即算出兩個質數的乘積，是非常容易的；而它本身，卻是非常困難的。這種“易守難攻”的特性，使它在密碼學中得到了重要的應用。

密碼學的基本框架，我們會在后面介紹量子密碼術時闡述。在這里，我們只需要指出一點：因數分解的困難性，是現在世界上最常用的密碼系統“RSA”的基礎。RSA這個名字，是三位發明者李維斯特（Ron Rivest）、薩莫爾（Adi Shamir）和阿德曼（Leonard Adleman）的首字母縮寫。

RSA是一種“公開密鑰密碼體系”，它的密鑰（即加密時用到的參數）是對全世界所有人公開的。為什么敢公開？因為這個密鑰是一個很大的合數，解密需要把它分解成兩個質數，而發布者有信心別人在正常的時間內解不開。

但是RSA有兩大隱患。第一點，我們只是知道目前公開的最好的算法是數域篩，但不知道是否有更好的算法。更令人寢食不安的是，某些國家、某些組織也許已經掌握解密的算法了，只是沒有告訴你！

第二點，上面說的算法都是在經典計算機上運行的，“最快的算法都無法破解RSA”指的是經典計算機。對于量子計算機，我們卻已經知道了它可以破解RSA。

如前所述，量子計算相對于經典計算有潛在的巨大優勢，只是實現這種優勢需要聰明的算法設計，只有對少數問題能夠設計出這樣的算法。而因數分解，就是這樣的問題之一。1994年，肖爾（Peter Shor）發明了一種量子算法，把因數分解的計算量減少到了多項式級別，也就是從不可計算變成了可計算。

艾數學同學，你又在舉手了？嗯，肖爾算法的計算量是O(n^2 logn loglogn)，一般人我不告訴他。

這又是個什么概念呢？同樣還是分解300位和5000位的數字，量子算法會把所需時間從15萬年減到不足1秒鐘，從50億年減到2分鐘！對RSA密碼系統來說，這不是“隱”患，而是“明”患！

看起來，全世界的密碼人員都應該陷入恐慌了。但事實上還沒有，人們仍然在用著RSA。為什么呢？因數分解的量子算法只是理論，真要實現它還是非常困難的，造出有實用價值的量子計算機還需要很多努力。

第一次真正用量子算法分解質因數是在2007年實現的，把15分解成3 × 5。有兩個研究組同時做出了這個實驗，一個是中國科學技術大學的潘建偉和陸朝陽等人，一個是澳大利亞布里斯班大學的A. G. White和B. P. Lanyon等人。此后各國科學家不斷努力，把這個領域推向前進。目前在實驗上分解的最大的數是291,311 = 523 × 557，是由中國科學技術大學的杜江峰和彭新華等人在2017年實現的。

什么，你前邊跟我說量子算法隨隨便便就能分解幾千位的數字，結果實際上最大只能分解一個六位數？你是在耍我嗎？

這位同學，請你先把手里的刀放下……同學們，一定要分清潛力和現狀。火車剛出現的時候，跑得沒有馬車快，還經常出故障。但是任何有洞察力的人都能看出，火車代表著未來，因為它能夠達到的上限遠遠超過馬車。RSA現在當然還可以用，但達摩克利斯之劍已經懸掛起來了，任何有責任心的密碼人員都會時刻關心量子計算的進展。

還有一點值得注意的是，造出專門處理某些任務的“專用”的量子計算機比造出“通用”的量子計算機要容易得多。專用的東西比通用的容易造，這是一個普遍規律。在可編程的電子計算機出現之前300多年，岡特（Edmund Gunter, 1581-1626）和奧特雷德（William Oughtred, 1574-1660）就造出了計算尺。

谷歌宣布計劃在2017年造出超越傳統計算機的量子計算機，很可能指的就是這種專用計算機。斯諾登從美國出逃后，披露了美國國家安全局有一個絕密的項目“穿透硬目標”（Penetrating Hard Targets），計劃建造一臺專用于破解密碼的量子計算機。據傳該局已經存放了大量外國政府的密電，一旦項目成功立刻對它們動手。這足以讓其他國家不寒而栗了！

同樣的道理，2017年5月，中國科學技術大學潘建偉和陸朝陽等人宣布造出世界上第一臺超越早期電子計算機的光量子計算機，也是特別針對一個問題的，這個問題叫做“玻色子取樣”。對它的量子算法，也是把指數增長的計算量縮減到了多項式增長的計算量。成果就是，這臺量子計算機算起玻色子取樣來，比第一臺電子管計算機ENIAC和第一臺晶體管TRADIC快了10到100倍。

順便提一下，有些人迷惑光量子計算機跟量子計算機是什么關系，甚至還有人說光量子計算機不是量子計算機。實際上，量子計算機總需要用某種物理體系來實現，好比電子計算機可以用電子管實現，也可以用晶體管實現，甚至可以像《三體》中設想的那樣用幾千萬人來實現（秦始皇：有人叫我？）。光量子計算機就是用光子作為量子比特的量子計算機。除了光子之外，量子計算機常用的物理體系還包括光學共振腔、離子阱、核磁共振等等。沒關系，你不需要現在就看懂這些物理學術語……

以后如果你看到量子計算機的新聞，千萬不要問“計算能力跟我的電腦比起來怎么樣”或者“打游戲會卡嗎”，人家一聽就知道你很外行。如果你問“它針對的是哪個數學問題，把計算量從什么改進到了什么”，人家就知道你是懂行的了。——一般人我不告訴他！

（未完待續）

背景簡介：本文作者為袁嵐峰，中國科學技術大學化學博士，中國科學技術大學合肥微尺度物質科學國家實驗室副研究員，科技與戰略風云學會會長。